Richard has a new preprint on ArXiv titled “Self-stabilized Bose polarons”!

Abstract:

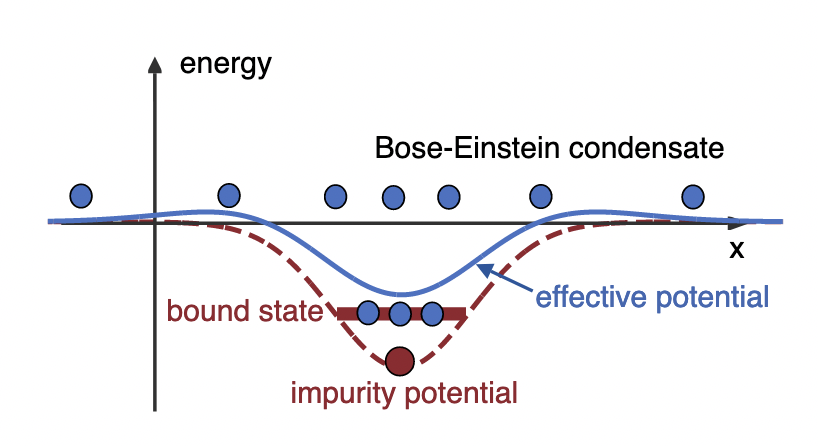
The mobile impurity in a Bose-Einstein condensate (BEC) is a paradigmatic many-body problem. For weak interaction between the impurity and the BEC, the impurity deforms the BEC only slightly and it is well described within the Fröhlich model and the Bogoliubov approximation. For strong local attraction this standard approach, however, fails to balance the local attraction with the weak repulsion between the BEC particles and predicts an instability where an infinite number of bosons is attracted toward the impurity. Here we present a solution of the Bose polaron problem beyond the Bogoliubov approximation which includes the local repulsion between bosons and thereby stabilizes the Bose polaron even near and beyond the scattering resonance. We show that the Bose polaron energy remains bounded from below across the resonance and the size of the polaron dressing cloud stays finite. Our results demonstrate how the dressing cloud replaces the attractive impurity potential with an effective many-body potential that excludes binding. We find that at resonance, including the effects of boson repulsion, the polaron energy depends universally on the effective range. Moreover, while the impurity contact is strongly peaked at positive scattering length, it remains always finite. Our solution highlights how Bose polarons are self-stabilized by repulsion, providing a mechanism to understand quench dynamics and nonequilibrium time evolution at strong coupling.

New preprint: Self-stabilized Bose polarons

• R. Schmidt, T. Enss, Self-stabilized Bose polarons,  arXiv:2102.13616