Our very own Marcel Gievers has a new preprint on arXiv about Flow equations for mfRG (multiloop functional renormalization group) in the so called SBE (single-boson exchange) parametrization!

Abstract:

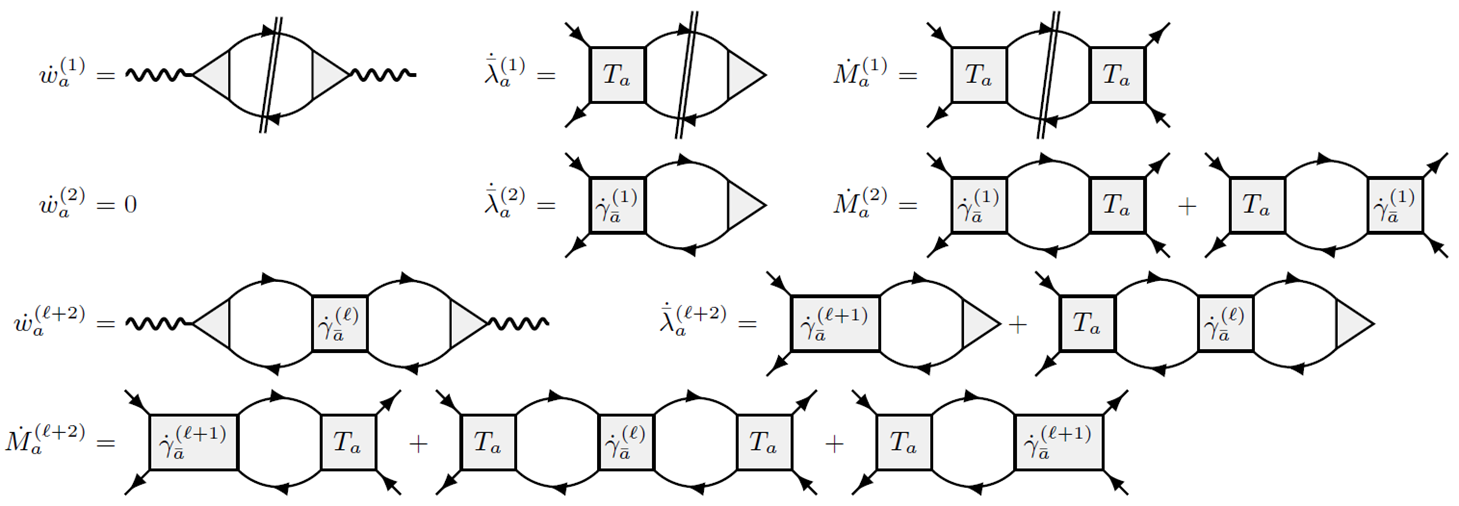
The recently introduced single-boson exchange (SBE) decomposition of the four-point vertex of interacting fermionic many-body theories constitutes a conceptually and computationally appealing parametrization of the vertex. It relies on the notion of reducibility of vertex diagrams with respect to the bare interaction U, instead of a classification based on two-particle reducibility within the widely-used parquet decomposition. Here, we construct a general form of the SBE decomposition following from the parquet equations, and derive multiloop functional renormalization group (mfRG) flow equations for the constituents of this SBE decomposition. Along the way, we also derive mfRG flow equations for the often-used decomposition of the vertex in terms of asymptotic classes of the two-particle reducible vertices. We show that the two decompositions are closely related, with mfRG flow equations very similar in structure.

Multiloop flow equations for single-boson exchange fRG

• Elias Walter, Marcel Gievers, Anxiang Ge, Jan von Delft, Fabian B. Kugler, Multiloop flow equations for single-boson exchange fRG, [ arXiv:2201.04878]